Rのflexmixパッケージで混合分布モデルによるクラスタ分析を行う。
Rで混合分布クラスタリングを行うときに有名なパッケージとしてflexmixが存在します。この記事ではflexmixの簡単な使い方を解説します。
flexmix自体は潜在クラス回帰を行うパッケージなのですが、混合分布クラスタリングを行うことも出来ます。
flexmixはRのglmクラスを用いてモデルを表現出来るため、他のパッケージに比べて柔軟なモデリングが可能というメリットがあります。
そもそも、混合分布クラスタリングとはなんぞやという人は以下の本文を参考にしてください。
1.モデルベースのクラスタリングとは
クラスタリングは代表的なものとして、以下の3つの方法が存在します。
おそらくk-meansと階層的クラスタ分析はみなさんご存知でしょう。
| 分類 | メリット・デメリット | 手法 |
|---|---|---|
| 階層的手法 | +データを樹形図として表現可能 ‐データ数が多いと、樹形図として表現できないのでデータ数が絞られる。 |
階層的クラスタ分析 |
| 分割的手法 | +代表点を入手可能 ‐代表点以外のデータの関係性やモデルに関する知識が得られない。 |
k-means PAM |
| モデルベース手法 | +データの発生メカニズムを知ることが出来る。 ‐事前にある程度のデータ発生メカニズムについて知る必要がある。 |
混合分布モデル |
混合分布を用いたクラスタリングはクラスタリングをする際にモデル構築するため、モデルベースのクラスタリングに属します。
階層的クラスタリングのようにデータ間距離の設定などがいらず、すべて確率という尺度に直した上で、クラスタリングできる。
またデータ発生メカニズムを知ることができるため成功すれば、非常に強力な手法であると言えます。
2.混合分布を用いたクラスタリング
混合分布を用いたクラスタリングについては@sleipnir002さんが、TokyoRで発表された以下のスライドを参考にしてください。
ちなみにこれは以下の本を参考にしているとのことなので、こちらの本の第4章も参考にしてください。

- 作者: 金森敬文,竹之内高志,村田昇,金明哲
- 出版社/メーカー: 共立出版
- 発売日: 2009/10/23
- メディア: 単行本
- 購入: 5人 クリック: 61回
- この商品を含むブログ (11件) を見る
3.混合分布一般によるクラスタリングへ
上記で紹介している手法はパッケージMClustを用いているため、データ発生メカニズムとしては正規分布しか用いることができません。
私は小売向けのアナリストですが、回数のデータなんかはポワソン分布だし、性別比とかは二項分布だし、正規分布だけだと色々と厳しいのが実情です。
そこで、もっと柔軟にモデルを表現する必要があります。
4.Rでの実行例
flexmixは潜在クラス回帰を行うためのパッケージですが、入力するglmのモデル式の形を工夫することで、混合分布クラスタリングを行うことが出来ます。
flexmixを実行して、クラスタ分析を行う例を用いて解説しましょう。
library(flexmix) #A.ポワソン分布×2と正規分布変数のデータ(y1,y2,y3)を作成 #クラスタ数は3(100, 100, 20) y1<-c(rpois(100, 3), rpois(100, 8), rpois(20, 6)) y2<-c(rpois(100, 10), rpois(100, 0.5), rpois(20, 6)) y3<-c(rnorm(100, mean=200, 15), rnorm(100, mean=200, 10),rnorm(20, mean=200, 10)) class<-c(rep(1, 100), rep(2, 100), rep(3, 20)) data<-data.frame(y1,y2,y3, class) rm(y1, y2, y3, class) #y1 barplot(table(data[, c(4,1)])) #y2 barplot(table(data[, c(4,2)])) #y3 plot(data[, 3], col=data[,4]) #B.混合分布モデルのコンポーネントをそれぞれ作成 Model_1<-FLXMRglm(y1 ~ 1,family="poisson") Model_2<-FLXMRglm(y2 ~ 1,family="poisson") Model_3<-FLXMRglm(y3 ~ 1,family="gaussian") #C.EMアルゴリズムの実施 mp<-flexmix(. ~ ., data=data, k=3, model=list(Model_1, Model_2, Model_3), control=list(verbose=1, nrep=5)) # Classification: weighted # 1 Log-likelihood : -2405.1507 # 2 Log-likelihood : -2173.0186 # 3 Log-likelihood : -1936.5001 # 4 Log-likelihood : -1911.7593 # 5 Log-likelihood : -1905.8872 # 6 Log-likelihood : -1903.8647 # 7 Log-likelihood : -1902.4038 # 8 Log-likelihood : -1901.2357 # 9 Log-likelihood : -1900.3630 # 10 Log-likelihood : -1899.6985 # 11 Log-likelihood : -1899.1289 # 12 Log-likelihood : -1898.5728 # 13 Log-likelihood : -1897.9860 # 14 Log-likelihood : -1897.3486 # 15 Log-likelihood : -1896.6569 # 16 Log-likelihood : -1895.9206 # 17 Log-likelihood : -1895.1609 # 18 Log-likelihood : -1894.4037 # 19 Log-likelihood : -1893.6678 # 20 Log-likelihood : -1892.9590 # 21 Log-likelihood : -1892.2749 # 22 Log-likelihood : -1891.6134 # 23 Log-likelihood : -1890.9800 # 24 Log-likelihood : -1890.3919 # 25 Log-likelihood : -1889.8763 # 26 Log-likelihood : -1889.4597 # 27 Log-likelihood : -1889.1529 # 28 Log-likelihood : -1888.9460 # 29 Log-likelihood : -1888.8157 # 30 Log-likelihood : -1888.7373 # 31 Log-likelihood : -1888.6915 # 32 Log-likelihood : -1888.6652 # 33 Log-likelihood : -1888.6502 # 34 Log-likelihood : -1888.6417 # 35 Log-likelihood : -1888.6369 # 36 Log-likelihood : -1888.6342 # 37 Log-likelihood : -1888.6327 # converged #D.サマリを表示する。 summary(mp) # Call: # flexmix(formula = . ~ ., data = data, k = 3, model = list(Model_1, Model_2, Model_3), control = list(verbose = 1, # nrep = 5)) # # prior size post>0 ratio # Comp.1 0.436 94 135 0.696 # Comp.2 0.445 100 117 0.855 # Comp.3 0.119 26 194 0.134 # # 'log Lik.' -1888.633 (df=14) # AIC: 3805.265 BIC: 3852.776 #E.パラメータを取得する。 parameters(mp) # [[1]] # Comp.1.coef.(Intercept) Comp.2.coef.(Intercept) Comp.3.coef.(Intercept) # 0.9826601 2.1248895 1.7702220 # # [[2]] # Comp.1.coef.(Intercept) Comp.2.coef.(Intercept) Comp.3.coef.(Intercept) # 2.3623702 -0.6625998 1.6267241 # # [[3]] # Comp.1 Comp.2 Comp.3 # coef.(Intercept) 200.23493 202.094819 200.380162 # sigma 15.13504 9.412856 5.797705 #F.交差表の作成 table(clusters(mp), data$class) # # 1 2 3 # 1 91 0 3 # 2 0 98 2 # 3 9 2 15 #G.結果のプロット plot(mp)
A.ポワソン分布×2と正規分布変数のデータ(y1,y2,y3)を作成
今回、y1、y2、y3という3つの変数をクラスタ分析にかけます。
変数は以下の分布に従うとします。
| 変数名 | 分布 |
|---|---|
| y1 | ポワソン分布 |
| y2 | ポワソン分布 |
| y3 | 正規分布 |
例えば、小売の顧客分類で例えると、y1は来店回数、y2商品の購入数、y3は利用金額(対数正規に従う)対数正規に従う利用金額の平均が200ってどうなの・・・とか言わないでください。といった例が考えうるでしょうか。
また、このデータには3つのクラス(クラスタ)がいて、それぞれ以下のようなパラメータを持っているとします。
| 変数名 | n(サイズ) | y1~λ | y2~λ | y3~μ | y3~σ |
|---|---|---|---|---|---|
| クラス1 | 100 | 3 | 10 | 200 | 15 |
| クラス2 | 100 | 8 | 0.5 | 200 | 10 |
| クラス3 | 20 | 6 | 6 | 200 | 10 |
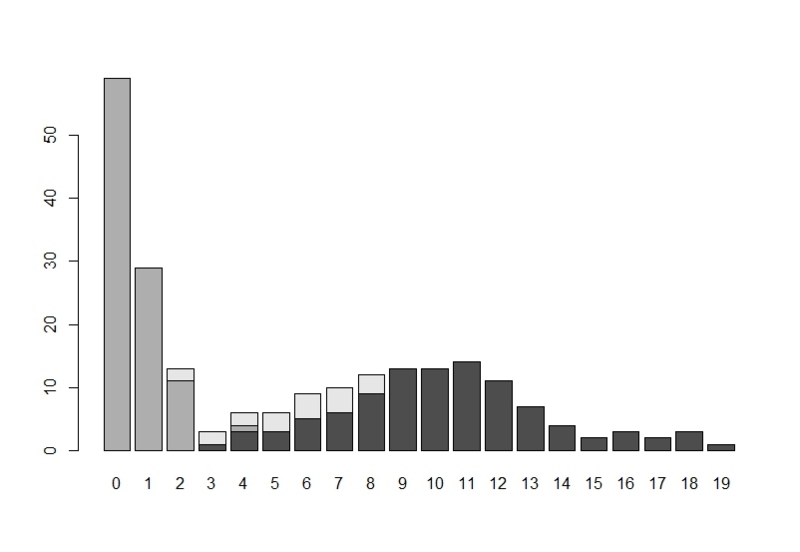
クラス別のy1のヒストグラムが以下の図です。

クラス別のy2のヒストグラムが以下の図です。
y3の値を各個体別にプロットしたが以下の図です。
(左からクラス1、2、3と続いています。)

B.混合分布モデルのコンポーネントをそれぞれ作成
ここでは、flexmixに入力するモデル式をglm形式で、作成しています。
ポイントは回帰式の説明変数が定数で、被説明変数が各変数yに対応しているということです。
C.EMアルゴリズムの実施
flexmix関数でEMアルゴリズムを実施して、混合分布モデルによるクラスタリングを行います。
kは想定しているコンポーネントの数を、modelには先ほど作成したglmモデルをリスト化して代入します。
controlはアルゴリズムのチューニング用です。
convergedと表示されていれば収束しています。
D.サマリを表示する。
summaryで実行結果のサマリを閲覧することが出来ます。
E.パラメータを取得する。
parametersで推定された各クラスタ毎のモデルのパラメータを見ることができます。
リストの1から順に、y1(Model_1)、y2(Model_2)、y3(Model_3)のパラメータを返しています。
(ポワソン分布のパラメータは対数です。)
実際のクラス別のパラメータ
| 変数名 | n(サイズ) | y1~λ | y2~λ | y3~μ | y3~σ |
|---|---|---|---|---|---|
| クラス1 | 100 | 3 | 10 | 200 | 15 |
| クラス2 | 100 | 8 | 0.5 | 200 | 10 |
| クラス3 | 20 | 6 | 6 | 200 | 10 |
推定されたクラス別のパラメータ
| 変数名 | n(サイズ) | y1~λ | y2~λ | y3~μ | y3~σ |
|---|---|---|---|---|---|
| クラス1 | 94 | 2.671553 | 10.61608 | 200.23493 | 15.13504 |
| クラス2 | 100 | 8.371972 | 0.5155094 | 202.094819 | 9.412856 |
| クラス3 | 26 | 5.872157 | 5.087182 | 200.380162 | 5.797705 |
F.交差表の作成
clusters(mp)でデータの属するクラスの値を取得出来ます。
これを実際のdataの属するクラスと比較しています、クラス3に多少の誤差はあるものの、分類できているようです。
G.結果のプロット
結果をplot関数に投げると、各クラスのクラス事後確率のヒストグラムが表示されます。

というわけで、flexmixの簡単な使い方を紹介ました。
細かなパラメータ設定についてはマニュアルを参照してください。
また、ガイドが結構丁寧なので、この記事を読まれて興味を持たれた方はぜひこちらを参照してください。
参考
FlexMix: A General Framework for Finite Mixture Models and Latent Class Regression in R
FlexMix Version 2: Finite Mixtures with Concomitant Variables and Varying and Constant Parameters